Intelligent Practice: 10 tips to supercharge it in the classroom

Ideas to improve one of my favourite task structures

Mar 12, 2024

This newsletter is made possible because of Eedi. Check out our brand-new set of diagnostic quizzes, videos, and practice questions for every single maths topic, ready to use in the classroom, and all for free, here.

Welcome to a series of posts where I will share 10 ideas to supercharge some of my favourite student practice activities. We will cover:

Venn Diagrams
SSDD Problems
Intelligent Practice (this post)
A little bit of problem-solving in each lesson

If you find these posts useful, the best way to support this newsletter is to share it with your colleagues. Thanks so much!

Intelligent Practice

I am a big fan of what I call Intelligent Practice. So much so, that I wrote a book about it, and built a website to share the sequences I have created and house those that have been created by teachers all around the world. Here is one of my favourites:

The basic idea

Intelligent Practice is a type of practice where consecutive questions are carefully related to each other. Usually, just one thing has changed between one question and the next. In the example above, a single yellow counter has been added to the example in Question 2 to give the example in Question 3. The challenge for students is to think about what impact that change will have on their answers.

Why Intelligent Practice is a good idea

The key principle underpinning Intelligent Practice is summed up by the following quote:

When certain aspects of a phenomenon vary when its other aspects are kept constant, those aspects that vary are discerned (Lo, Chik & Pang, 2006)

By holding constant as much as possible and varying one element, we can direct students’ attention to that element that has varied. Any change (or lack of) in the answer or approach to getting the answer may then be attributed to the change in the element. Moreover, because each example is related to the one that preceded it, students can form expectations as to what the answer will be. I call this process Reflect, Expect, Check, Explain. This can lead to significant moments of revelation and discussion when these expectations are not realised, compelling students to think more deeply about the processes involved, instead of just cruising through a sequence of questions on autopilot.

Intelligent Practice: 10 top tips

Fluency practice comes first. Before taking on Intelligent Practice, give your students some questions on the topic that are not related to each other. During Intelligent Practice we are asking students to pay attention to two things: the procedure needed to solve the problem, and the relationships between examples. If students do not have a certain competence and confidence with the procedure, they will be unable to attend sufficiently to the relationships and thus not get much out of Intelligent Practice. A few warm-up questions on the topic where students do not need to think about the relationship between them will help.
Support students to Reflect. Just before students dive into working out the answer to a problem in an Intelligent Practice sequence, we need to encourage them to pause and Reflect. For example, take the following pair of questions from a sequence on estimating the mean from grouped frequency:

The student has worked out that the answer to Question 5 is 50kg. Before they dive straight into working out Question 6, we need them to pause and ask themselves: What has changed, and what has stayed the same? This brief moment of reflection sets up everything that follows.

Support students to Expect. Based on what they noticed during their reflection, can students form an expectation about how the answer to Question 6 might change? Will it be greater than 50kg, less than 50kg, or equal to 50kg? Some students might like to put a specific number on it. One of the benefits of the Expect phase is it makes these examples mean more to students. Having formed an expectation, students are now very keen to find out if they are correct or not - they have skin in the game. Many students, understandably, struggle with the Expect stage of the process, so here are some support prompts I use to help students:

Support students to Check. We now need to ensure that students carry out the algorithm. Some students will be keen to skip out this stage, so certain as they are in their expectations. So, we must circulate and check students are setting their working out as we have asked and not taking shortcuts.

Support students to Explain. This is the fun part. Once students have worked out the answer, one of three scenarios could occur, and for each, we need to support them in their thinking:

Use the 4-2 approach. This is where students work on their own, in silence, for 4 minutes, and then have 2 minutes of collaboration with their partner, before the cycle repeats. I find 4 minutes is sufficient time for students to do some thinking on their own without being dominated by an eager partner (there is nothing worse than someone telling you about the relationship before you have had a chance to think for yourself), and 2 minutes is sufficiently short for the students to have a positive, focused paired discussion to compare their reflections, expectations, answers and their explanations.
Consider doing this with the whole class at the same time. The approach I have described so far is aimed at students working independently through a sequence of questions. But you can also run Intelligent Practice sequences to the whole class, controlling the pace by only revealing one example at a time. For example, consider this sequence from the OUP Mosiac maths series that I have series edited:

Project the first question on the board and ask students to work out the perimeter, which is 28:

Then we can project the next example on the board, next to it:

Students can be prompted to reflect on what has changed, and then form an expectation about what happens to the perimeter (does it increase, decrease, or stay the same), and show this on their mini-whiteboards. Students can then put their boards together, and share their reasoning with their partner, before checking their answers and continuing the discussion as they seek to explain what has happened.

The advantages of this approach are that you can direct all students to Reflect, Expect, Check and Explain, and coordinate a discussion where students hear the thinking of several of their classmates. The disadvantage is that not everyone works at the same speed, so you are likely to move too quickly for some, and too slowly for others. Doing the first few questions with the whole class and then switching to independent mode is a nice way to get the best of both worlds.

Consider asking students to explain just one relationship. In the early days, I used to ask students to write me a sentence for Reflect, a sentence for Expect, show all their working for Check, and then potentially a paragraph for Explain. This was too much for some students, took too long, and got in the way of their mathematical thinking. Now, I ask students to form reflections and expectations in their head, show all their working out, pause to explain, and then move on. But at the end of the sequence, I will ask students to write up their explanation for one relationship. This will either be one I have chosen in advance (so everyone does the same, and we can discuss afterwards), or one each student selects (so they can choose the one they feel most confident in explaining, and thus have more buy-in).
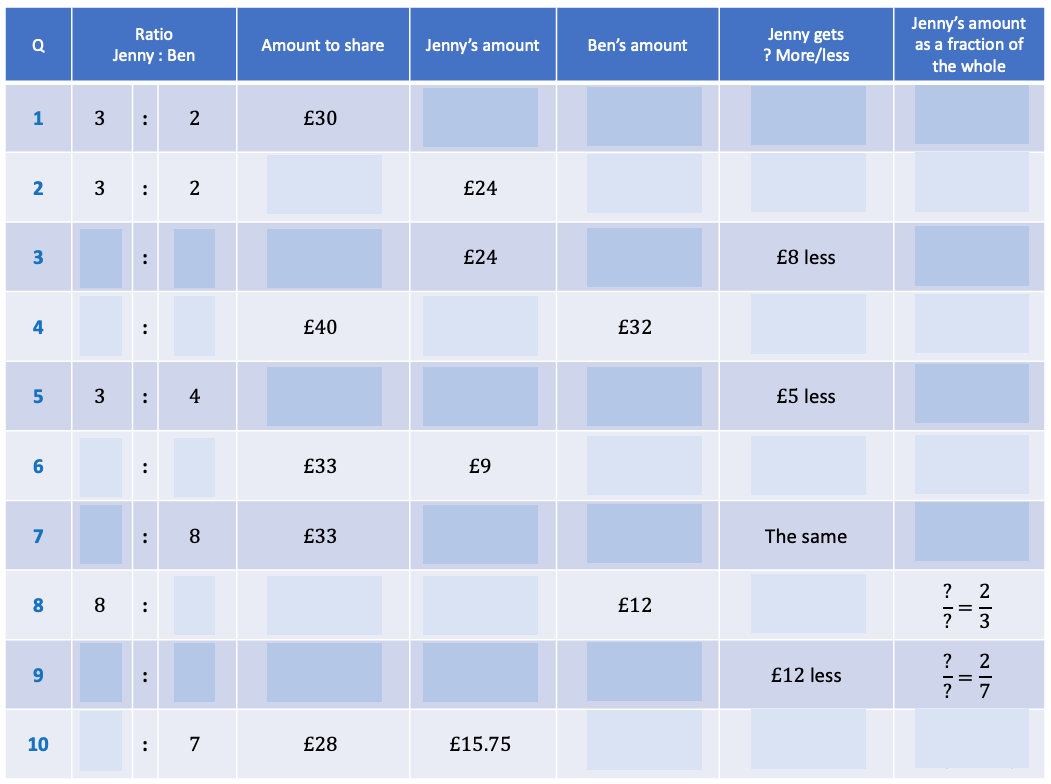
Try a Fill in the Gaps activity. A popular variation of Intelligent Practice sequences are Fill in the Gaps activities. These are exactly as you would imagine, with the only difference being that relationships exist between the rows, so we need to prompt students to pause and Reflect after each completed row before they dive into the next. Here is one of my favourites:

Try a Variation Spider activity. Another spin-off! This time, each example on the outside of the spider is related to the example in the middle. Students also have a challenge in the bottom-left corner where they must come up with the question, and a challenge in the bottom-right corner where they must come up with a related question and answer. I like this one:

Three of my favourite Intelligent Practice activities:

Challenge your students with some of these… or enjoy trying them yourself. And remember, you can find all my Intelligent Practice activities here, and read more about how I use them in my Reflect, Expect, Check, Explain book.

Fractions of an amount: