The best maths worksheet ever?

A worksheet structure to really check the depth of your students' understanding

Hello!

I hope you are well, and basking in post-exam bliss… okay, that might be pushing it a bit.

Now, one thing I love is a structure that I can use across many topics and with many classes. It is why I am such a big fan of diagnostic questions, Venn Diagrams and Give an example of.

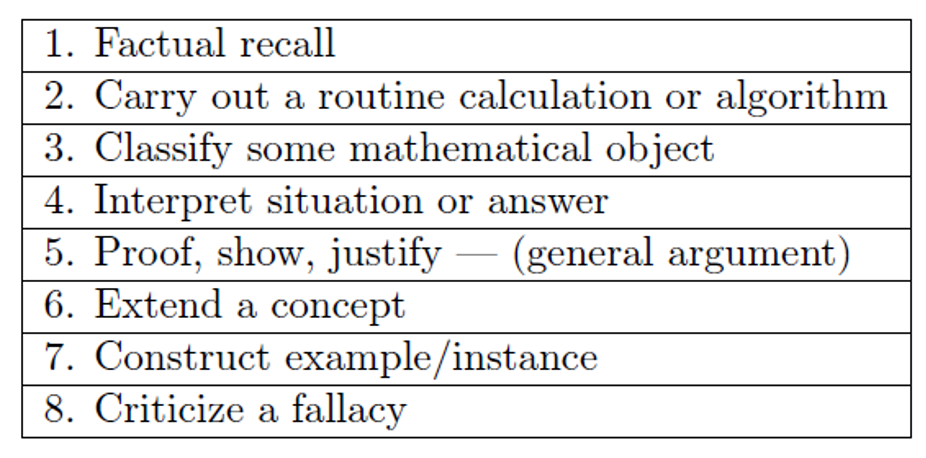
I also have a favourite worksheet structure (don’t we all?) that uses a taxonomy of question classification proposed by Pointon and Sangwin in their 2003 paper An analysis of undergraduate core material in the light of hand-held computer algebra systems. The taxonomy looks like this:

All of this is very abstract, so let’s make it concrete with a fantastic example of how this framework can be applied to create a set of questions on the highest common factor, produced and shared by Dan Lewis:

Let’s analyse each category of question, illustrating them with Dan’s example:

1. Factual recall

Example: The common factors of two integers are 1, 2, 3, 6 and 12. What is the highest common factor?

Factual recall needs to come before carrying out a procedure. Do students know what they are actually trying to work out? Do they have the prerequisite knowledge to engage with the new idea?

2. Carry out a routine calculation or algorithm

Example: Find the highest common factor of 18 and 30

This is the most common question type on most worksheets. And for good reason, because fluency in carrying out calculations is important. But there is a lot more to maths than this.

3. Classify some mathematical object

Example: I have an odd integer and an even integer. Which of the following could be common factors: 1, 2, 3, 4?

I am not a huge fan of technical definitions. I much prefer the challenge to classify. Can students sort the examples from the non-examples given some criteria?

4. Interpret a situation or answer

Example: If the highest common factor of two numbers is 6, are both integers even, both odd, or one odd and one even?

The idea of giving the answer and asking what you can infer about the question is a powerful one, flipping the usual way of working on its head. Similarly, we could challenge students to interpret a situation by adding a context to the question that students need to unpick to get at the mathematics.

5. Proof, show, justify

Example: Show, with some examples to help, that the highest common factor of two consecutive integers is always 1

Proof does not need to be in the formal, algebraic sense. But questions like these encourage students to try examples in a logical, systematic way as they construct their arguments. For many students, this may be the first time they realise something very special about mathematics: you can generalise! In other words, if we are careful about our choices of examples, we can make arguments that we know will apply to any possible number, even though we haven’t tested it.

6. Extend a concept

Example: Find the highest common factor of 12, 18 and 20

Here we have an opportunity to push the concept a little further. That may mean introducing more challenge to the procedure (as in the example above), or it could mean weaving in different areas of mathematics.

7. Construct an example/instance

Example: Find a pair of integers with a highest common factor of 8

I am obsessed with asking students to construct their own examples based on certain constraints. You could use the Give an example of framework to make this category of question even more powerful.

8. Criticise a fallacy

Example: Ben says he has found two different odd integers with a highest common factor that is even. Explain why he is wrong.

Identifying and explaining mistakes is so important. Not only do they challenge students to think beyond carrying out a routine, but in their quest to interpret someone else’s work, they must also communicate mathematically. You could even go one further and tag on the end: and explain how you would help Ben understand.

Here is another example of the taxonomy, this time applied to the area of a trapezium, produced and shared by Middleton Maths:

One more? Go on then. Here is another from the wonderful Middleton Maths, this time on prime factorisation:

This structure could be used as a low-stakes assessment, a homework, or an independent task followed by paired collaboration. It is a great way of checking the depth of students’ understanding, and promoting key skills such as reasoning, conjecturing and mathematical communication.

The dream, of course, is you have one of these for every topic. Ben Gordon tried to crowdsource these in the build-up to last year’s GCSE exams, but the quality was mixed. These take time and effort to produce, but I genuinely believe the effort is worth it.

If I told my wife I am going to start yet another website that makes zero money, divorce would be on the cards (again). But if you are reading this and you agree with me that this is a super powerful worksheet structure, try to create one (and just one) for an upcoming topic, and share the link to it in the comments. This is a great activity to do as a department. If there is enough interest, then I will set up a site to host them, and we will go from there. Just don’t tell my wife.

Three final things from Craig

1. Have you listened to my recent conversation with Ollie Lovell, where we discuss connections, worked examples and iPads?

2. You can see the back catalogue of all my Eedi newsletters and Tips for Teachers newsletters here

3. Have you checked out my Tips for Teachers book, with over 400 ideas to try out the very next time you step into a classroom?

If you found this newsletter useful, subscribe (for free!) so you never miss an edition, share it with one of your colleagues, or let me know your thoughts by leaving a comment.

Thanks for reading and have a great week!