My variation theory website: new resources + new uses?

Three ways to use intelligently varied sequences of examples

Have you seen our brand-new small step quizzes for White Rose Maths Years 2 to 9? They are completely free.

Perhaps the most controversial thing I have done in my career (to date!) is launching my variationtheory.com website. It led to me:

1. Being called “the most dangerous and clueless man in maths education”

2. Writing my second book (Reflect, Expect, Check, Explain - still available in all good, and evil, bookstores) to explain myself

3. Stop sharing the free resources I create on social media because I could predict the comments from the usual suspects, and it was harming my mental health.

However, as of the time of writing, nearly 7.5 million people have visited variationtheory.com since its inception in 2019, which hopefully indicates that some people find it useful.

Over the past six years, I have refined the way I use the site's sequences of questions and examples. So, I thought I would share my current approach here and showcase some brand-new activities created by kind and generous teachers worldwide.

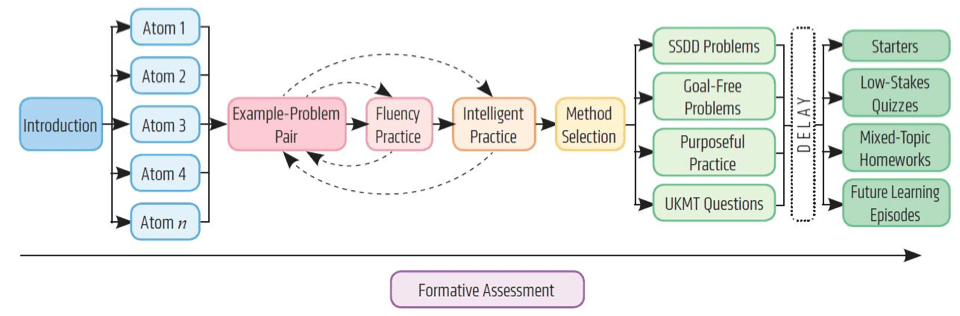
A model of a Learning Episode

When writing Reflect, Expect, Check, Explain, I introduced my model of a Learning Episode, defined as the amount of time needed for students to grasp a novel idea:

As you can see, Intelligent Practice—the name I gave to the type of practice typified by the sequences of examples on my website—comes after fluency practice and before method selection and problem-solving.

I have since refined this model of a Learning Episode, and it now looks like this:

I won’t go into the reasons for all the changes here - you can read about them here. However, the eagle-eyed among you will have noticed that Intelligent Practice is no longer there. So, where do the sequences of examples and activities on my variation theory website fit into this updated model of a Learning Episode?

Use case #1: Atomisation

Atomisation is breaking routines down into their smallest constituent parts (atoms) that can be assessed or taught separately from the routine itself.

The Rule sequences of examples and non-examples on my variation theory website are perfect for Atomisation.

Imagine we are planning a Learning Episode on the equations of straight-line graphs. As part of this, we want students to identify when an equation of a straight line is in a form that allows us to immediately determine the gradient and the y-intercept without rearranging the equation. This is an example of an Atom.

We can use this brand-new sequence of examples and non-examples from Dan Draper to teach and check our students’ understanding:

Students can indicate their answers on mini-whiteboards or with their thumbs. We can then quickly move on to more complex examples or diagnose any specific areas of misunderstanding.

I write more about Atomisation here.

Use-case #2: A sequence of We Dos

One of the most significant changes I have made to my practice over recent years is dedicating more time and attention to the We Do phases of a Learning Episode. In the past, following a teacher-led I Do, I would conduct a quick check for understanding and then set students off on independent work. Now, I like to keep the class together for as long as possible to gather more data about the depth of their understanding through a sequence of We Dos. The sequences of Practice questions on my variation theory website are perfect for this.

Take this brand-new sequence from Alex Ladell-Stuart.

Following a couple of quick teacher-led examples, students could be presented with this sequence, one question at a time, with students responding in unison on their mini-whiteboards.

Generally, I continue until the percentage of students who get the questions correct falls below 80%. When that happens, I can either address an issue with the whole class or assign a group of students to independent practice while I support the students who are struggling—and of course, because of the mini-whiteboards, I now know the exact nature of their misunderstandings.

I write more about the We Do here.

Use-case #3: Consolidation

When I observe lessons, the most common use case for the questions from my variation theory website is students working through them during independent practice. These sequences are particularly well-suited for independent work because students can access them at various levels.

I teach students to:

1. Reflect: ask how this question is related to the previous one

2. Expect: form an expectation about how the answer might be related to the previous one

3. Check: work out the answer using the procedure they have been taught

4. Explain: try to explain the relationship between the answer to this question and the previous question in a way that someone else would understand

Take this sequence of questions from Tom Williamson on the length of line segments:

Pay particular attention to the relationship between Questions 10 and 11.

Most students will notice that just the y-value of the second coordinate has changed. Some students will be able to form a prediction about what might happen to the length compared to Question 10 - whether it increases, decreases, or remains the same. Other students may not be able to form a prediction. Students can then work out the answer and potentially be surprised. All students—whether they were able to form an expectation or not—now have an opportunity to think hard about what is going on.

The key point is that we do not need to predict in advance what experience students will have. We do not need to differentiate in the sense of assigning different work to different students. Differentiation happens through experience, and students will surprise us—and themselves—with their insights.

I have written an entire book about maximising the effectiveness of these sequences during independent practice, and I share a summary of the key strategies on my page about Consolidation here.

In summary

Even though it caused me more mental anguish than anything else I have ever done professionally, I am still delighted I built my variation theory website. I want to take this opportunity to thank all the teachers who have submitted their work to me.

How do you use the sequences on the variation theory website?

What do you agree with, and what have I missed?

Let me know in the comments below!

🏃🏻‍♂️ Before you go, have you…🏃🏻‍♂️

1. … signed up for my free online workshop: 25 Tips for Teachers?

2. … read my latest Tips for Teachers newsletter about teaching with worked examples?

3. … listened to my most recent podcast about AI in education?

4. … read my write-ups of everything I have learned from watching 1000s of lessons?

Thanks so much for reading and have a great week!

Craig