Free resource - variation spiders!
A different way of using Intelligent Practice in your classroom
A few weeks ago I was working with a maths department that was trying to get their students to engage with what I call Intelligent Practice. These are sequences of questions where consecutive examples are related to each other in a certain way, and by encouraging students to think hard about these relationships we draw their attention to key concepts underlying mathematical ideas.
Here is an example of such practice where students are asked to find the nth-term rule of a set of linear sequences:
The issue that the department was having - and I have experienced this before - was that students were getting stuck early on in the sequence, and were therefore not able to make much progress.
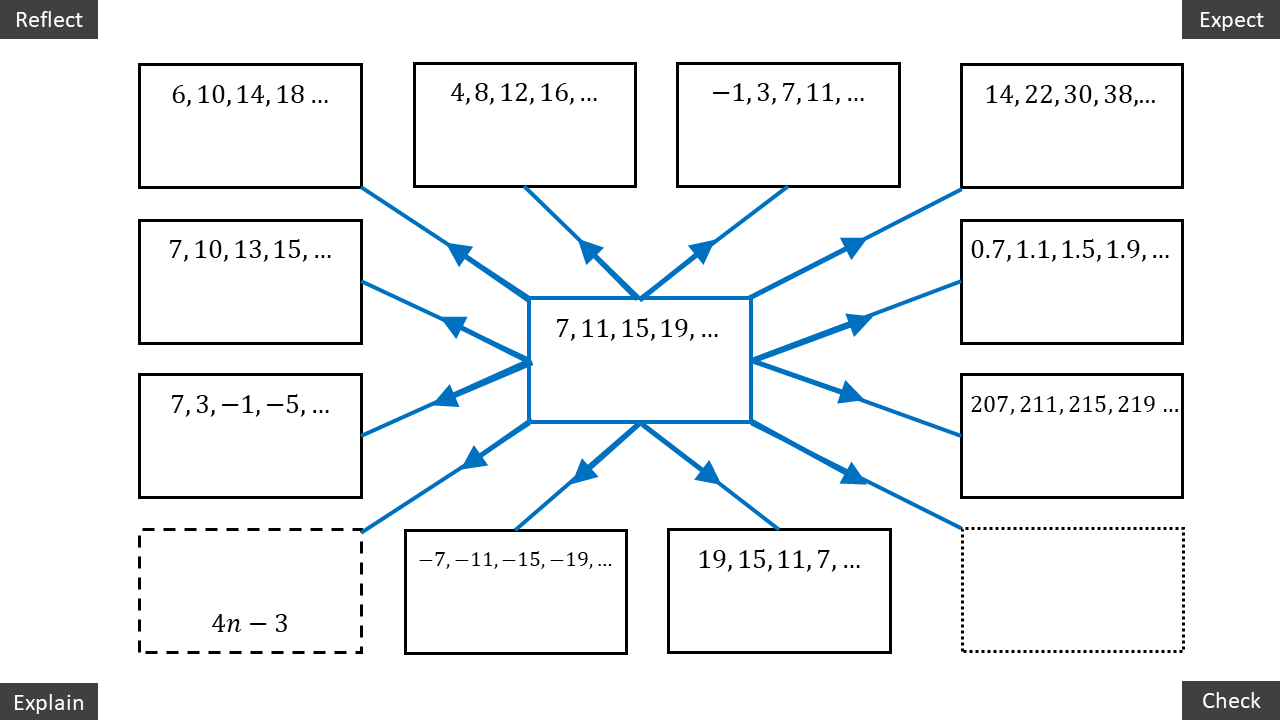
So, I decided to rework the structure of the activity, and change it into a spider:
Notice here that each example on the legs of the spider is related to the example in the body. So, once students establish the correct answer for the body - which could be done as a whole-class example and checked by the teacher - they are then free to pick and choose the relationships to consider around the outside. And if they get stuck on one, they can simply move on to another.
I printed out a copy of the spider for each student, and gave them the following instructions:
Do your working out in your book or on a mini-whiteboard and just write your final answer on the worksheet
Answer the question in the middle box
Chose one of the outer boxes – you can start anywhere you like
Reflect – how is this example the same and how is it different from the example in the middle?
Expect – based on what you noticed, can you predict anything about what the answer will be?
Check – work out the answer and write it in the box
Explain – If your expectation and check are different, can you understand the relationship now? If your expectation and check are the same, how would you explain the relationship to someone who doesn’t understand yet?
Now do the same approach with a different box
For the dashed box, can you change the example as little as possible to get this answer?
For the dotty box, create your own example by changing the example in the middle, and then do Reflect, Expect, Check, Explain
When you have finished (or the teacher tells you), choose the relationship you think you can explain the best and try to explain it as clearly as possible (use words, pictures, more examples… whatever you like!) to help someone who doesn’t understand it yet
This went really well. Students seemed to enjoy the format, and the inclusion of a learner-generated example produced some crackers that students could swap with their partners and check.
I decided to create a few more of these - what I am calling Variation Spiders - in case they are useful. So far we have:
Gradient and y-intercept of a straight line graph:
And - my personal favourite - angle at the centre circle theorem:
All of these sequences - plus 100s of others - are available on my Variation Theory website.
I hope you and your students find these spiders useful.
If you found this newsletter useful, subscribe (for free!), share it with one of your colleagues, or let me know your thoughts by leaving a comment. And if you have any questions, just hit reply!
Thanks so much for taking the time to read this
Craig