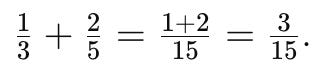Can AI chatbots write a good multiple-choice diagnostic question?
The capabilities of AI in September 2024 – Part 2
Do you set exclusively paper-based homework at your school and are state-funded and UK based? We’re looking for new schools to take part in our Year 7 research project to test the effectiveness of Eedi whilst doubling the rate of maths learning for disadvantaged students. If your school sounds like the perfect candidate, you have one week to apply by booking a call with the team by clicking here. There are 4 spaces left and it starts this month.
***
This is Part 2 of a trilogy of posts looking at AI's capabilities of supporting teachers with their planning as of September 2024. The posts are:
Can AI chatbots write a good multiple-choice diagnostic question? (This post)
Can AI chatbots plan a maths lesson?
I'm excited to revisit this series of posts in 12 months to see what advances have been made.
***
Introduction
I will test AI’s current capabilities to do three things that will aid teacher planning. And by aid, I am not just talking about saving time (which is, of course, important) but doing so without sacrificing - or by hopefully improving - the quality of the materials produced.
I will test AI’s current capabilities to perform what I consider to be three tasks of increasing complexity. Last week, we looked at anticipating student misconceptions. This week, let’s turn our attention to the creation of multiple-choice diagnostic questions.
Why is creating multiple-choice diagnostic questions important, and why is it hard?
Multiple-choice diagnostic questions are a great way of checking students’ understanding. They have three benefits over open-response questions:
You can gather students’ responses quickly in the classroom without needing technology. A simple set of ABCD cards or even fingers can be used, and every student can share their answer immediately.
You learn the specific nature of a student's misunderstanding from their choice of wrong answer. A child who chooses the wrong answer of C likely has a different misconception than the child who chooses the wrong answer of D. If you know why students are struggling, you can help them more effectively.
Whether you create the diagnostic question yourself or study it before the lesson, your mind naturally turns to thinking about the wrong answers: Why might a student select them? How will I respond if they do? Crucially, you can do this thinking outside the noise of the lesson, meaning you can step into the classroom better prepared.
However, a good multiple-choice diagnostic question is hard to write. You need all the skills and experience from last week’s challenge to anticipate the students' struggles. But then you need to translate each of those struggles into a choice of the wrong answer that a student who had that specific struggle would choose. This is tough… for me, at least.
My attempt
I reckon I have written over 10,000 multiple-choice diagnostic questions in the 10 years since I co-founded diagnosticquestions.com and Eedi. And to be honest, I need a break. So, if the AI chatbots can do a good job, then I am off to the beach.
Here is a multiple-choice diagnostic question I wrote a few years ago to assess students’ understanding of adding fractions:
Like any decent diagnostic question, the wrong answers are designed to identify the specific nature of students' misconceptions. Can you see why a student might go for each of the wrong answers?
Here is what I was thinking:
A: Believes you add the numerators and the denominators
B: Remembers that you need to make the denominators the same, but fails to adjust the numerators
C: Transforms the fractions correctly in a form ready to be added, but then adds the numerators and denominators in the final step
D: The correct answer
I am happy with this question from an author’s point of view. My experience in the classroom suggests it captures three of the most significant misconceptions students hold about adding fractions.
And the data supports this view. The question has been answered over 20,000 times on our diagnostic questions and Eedi websites, and here are the results:
Many students choose each wrong answer, and their explanations match my reasoning.
But what would an AI chatbot produce?
The AI Chatbots
Like last week, for this exploration, I used four of the most popular AI chatbots available at the moment:
All are free to use once registered.
The prompt
Here is the prompt I gave to all four chatbots:
I want you to write a multiple-choice diagnostic question. I want one correct answer and three incorrect answers. Each incorrect answer should reveal the specific misconception a student holds or the mistake they make. I want you to choose the three wrong answers to reveal the three most common misconceptions students may have or mistakes they might make, and I also want you to give me the reason a student might choose each of these wrong answers.
Using this guidance, please create a diagnostic question for 1/3 + 2/5
Chatbot #1: Gemini
Here is the output from Google’s AI chatbot, Gemini:
What is the sum of 1/3 + 2/5?
Options:
A. 3/8
B. 7/15
C. 5/8
D. 3/5
Reasoning for Incorrect Answers:
A. 3/8: This answer suggests that the student added the numerators and denominators separately, a common misconception when adding fractions.
B. 7/15: This answer indicates that the student correctly added the numerators but then added the denominators, another common mistake.
C. 5/8: This answer might be chosen if the student incorrectly assumed that the denominators need to be the same before adding and simply added the numerators and kept the denominator of 8.
On the positive side, Gemini has certainly created a multiple-choice question.
But then the problems begin.
Our first concern is the lack of a correct answer – given no explanation is offered for Option D, does Gemini believe 3/5 is the correct answer? Let’s ask them:
Me: Which option gives the correct answer?
Gemini: The correct answer is B. 7/15.
The student correctly added the numerators (1 + 2 = 3) but then added the denominators (3 + 5 = 8), which is incorrect. To add fractions with different denominators, you need to find a common denominator, which in this case is 15. Then, you can convert each fraction to an equivalent fraction with a denominator of 15 and add the numerators. So, 1/3 becomes 5/15 and 2/5 becomes 6/15. Adding the numerators (5 + 6 = 11) and keeping the common denominator gives us 11/15. However, 11/15 can be simplified to 7/15.
Hmmm…
Me: How can 11/15 be simplified to 7/15?
Gemini: You're absolutely right! There seems to be a mistake in my previous response. 11/15 cannot be simplified to 7/15.
The fraction 11/15 is already in its simplest form. There is no common factor greater than 1 that divides both 11 and 15.
Therefore, the correct answer to the original question, "What is 1/3 + 2/5?" is 11/15.
I apologize for the oversight. Thank you for catching my error!
We all make mistakes, I guess.
I also wanted to dig into Gemini’s choice of wrong answers. A is a good one. But the rest I don’t really understand. Seeing as it did not offer an explanation for D, I thought I would ask for one.
Me: Why might a student choose option D, 3/5?
Gemini: Option D, 3/5, might be chosen by a student who incorrectly assumes that they can simply add the numerators and denominators separately. This is a common misconception when adding fractions.
In this case, the student might think that 1 + 2 = 3 for the numerator and 3 + 5 = 8 for the denominator, resulting in the answer 3/8. However, this approach is incorrect because it doesn't take into account the need to have a common denominator before adding the fractions.
At this stage, I gave up.
Chatbot #2: ChatGTP
Here is the output for the same prompt from last week’s star pupil, Open AI’s chatbot, Chat GTP:
The first thing to note is we have a correct answer! Secondly, look how ChatGTP uses actual maths notation. Nice! It also does this in the explanations it offers:
Correct answer:
D: Explanation: The correct approach is to find a common denominator, which is 15, and then add the fractions:
Incorrect Answers and Misconceptions:
A: Reason a student might choose this: The student mistakenly adds the numerators and denominators directly without finding a common denominator first. This reflects the misconception that fractions are added by simply adding the top and bottom numbers:
B: Reason a student might choose this: The student correctly identifies the need for a common denominator but then only adds the numerators while keeping one of the denominators as it is. They might have incorrectly used the denominator of 15 directly without applying it to both fractions:
C: Reason a student might choose this: The student correctly identifies the need for a common denominator and adds the fractions but only adds the numerators incorrectly. They may have mistakenly used the numerators as they originally appear without adjusting them for the common denominator:
This is clearly much better than Gemini’s efforts. But notice Option D. Where has that 7 come from? Let’s ask it:
Me: I don’t understand why a student would write 7 for the numerator for Option C. Please could you explain?
ChatGTP: You're correct to question that; the reasoning for Option C having a numerator of 7 doesn't make sense as written. Let me clarify and correct that.
Revised Reasoning for Option C:
Reason a student might choose this: The student correctly finds a common denominator of 15 but incorrectly adds the adjusted numerators. Instead of properly adjusting the numerators by multiplying them with the factors needed to match the common denominator, the student adds the original numerators directly (1 and 2) after finding a common denominator, which yields 3. They then mistakenly add this sum to one of the numerators (either 1 or 2), leading them to the incorrect numerator of 7:
Maybe, I guess…
Chatbot #3: Co-pilot
Here is the output from Microsoft AI’s chatbot, Co-pilot for the same prompt:
A. ( \frac{3}{8} )
B. ( \frac{3}{15} )
C. ( \frac{7}{15} )
D. ( \frac{11}{15} ) (Correct Answer)
Yes, it’s the exact same answers as ChatGTP, in exactly the same order, just looking a bit worse for wear. As a teacher, my first question is: Who is copying who?
Let me tidy up the output:
A. 3/8
B. 3/15
C. 7/15
D. 11/15
Now let’s see Co-pilot’s explanations:
Explanation of Incorrect Answers:
A. 3/8: This answer results from incorrectly adding the numerators and denominators directly, i.e., 1/3 + 2/5 = 3/8. This reveals a misconception that fractions can be added by simply adding the numerators and denominators.
B. 3/15: This answer comes from multiplying the numerators and denominators together, i.e., (1 x 2)/(3 x 5) = 2/15. This shows a misunderstanding of the addition of fractions, confusing it with multiplication.
C. 7/15: This answer is obtained by adding the fractions without finding a common denominator, i.e., 1/3 + 2/5 = (1 + 2)/(3 + 5) = 3 / 8. This indicates a misconception that fractions can be added directly without converting to a common denominator.
Correct Answer:
D. 11/15: To add 1/3 and 2/5, you need to find a common denominator. The least common denominator of 3 and 5 is 15. Converting the fractions, we get 1/3 = 5/15 and ( 2/5 = 6/15. Adding these gives 5/15 + 6/15 = 11/15
Again, the output all looked like this: ( \frac{11}{15} ), so I had to tidy it all up. Putting that aside, read that weird explanation for our friend 7/15. Let’s push Co-pilot on this:
Me: I don’t understand why a student would write 7 for the numerator for Option C. Please could you explain?
Co-pilot: I see how that might be confusing. Let me clarify:
Option C, 7/15, is actually a mistake on my part. The correct misconception should be represented by 3/8, which I already used in Option A.
To correct this, let’s revise the question:
Co-pilot then gave the exact same answers, in the same order, but with a new explanation for Option C:
This answer might come from a student incorrectly finding a common denominator but then adding the numerators incorrectly. They might convert 1/3 to 5/15 and 2/5 to 6/15, but then mistakenly add the numerators as ( 5 + 2 = 7 ) instead of ( 5 + 6 = 11 ).
Co-pilot seemingly hallucinates in the exact same way at ChatGTP, profusely apologises for its mistake, and then corrects itself in the same way.
Something weird is going on there.
Chatbot #4: Claude
Claude is not one for small talk and dives straight in:
Here's a multiple-choice diagnostic question for 1/3 + 2/5, along with an analysis of each incorrect answer:
What is the sum of 1/3 and 2/5?
A) 3/8 B) 3/15 C) 11/15 D) 5/8
Correct answer: C) 11/15
Analysis of incorrect answers:
A) 3/8 Reason: A student might choose this answer if they simply add the numerators and denominators separately without finding a common denominator. This reveals a fundamental misunderstanding of fraction addition. (1+2)/(3+5) = 3/8
B) 3/15 Reason: A student might select this if they correctly find the common denominator (15) but then incorrectly add only the original numerators without adjusting them to the new denominator. This shows a partial understanding of the process but a crucial error in execution. (1+2)/15 = 3/15
D) 5/8 Reason: A student might choose this answer if they correctly convert the fractions to a common denominator (40) and add the numerators (25+32=57), but then simplify incorrectly by dividing both the numerator and denominator by 7 instead of 3. This reveals a mistake in the final simplification step. 57/40 simplified incorrectly to 5/8
The choice of answers and the explanations given for A and B are great. But D is a bit dodgy. I am not sure where the common denominator of 40 comes from, then where the 25 and 32 come from, why they would divide by 7, why Claude thinks 3 is a better choice, and how 57/40 becomes 5/8.
I decided to give Claude one more chance:
Me: I don’t understand your explanation for D. Please could you try again?
Claude: I apologize for the confusion in my previous explanation for option D. You're right to ask for clarification. Let me provide a clearer and more accurate explanation for why a student might choose 5/8 as their answer.
Revised explanation for D) 5/8:
Reason: A student might arrive at this answer through the following incorrect process:
They correctly recognize that they need to find a common denominator.
They might choose 8 as the common denominator (incorrectly thinking it's the least common multiple of 3 and 5).
They then attempt to convert each fraction to an equivalent fraction with denominator 8: 1/3 → 3/8 (incorrectly multiplying both numerator and denominator by 3) 2/5 → 2/8 (incorrectly multiplying only the denominator by 2)
Finally, they add the numerators: 3/8 + 2/8 = 5/8
This mistake reveals several misconceptions:
Incorrectly identifying the least common multiple of the denominators
Misapplying the rules for creating equivalent fractions
Not recognizing that their result is greater than 1/2, which the correct sum should be
Thank you for asking for clarification. This explanation better represents a plausible mistake a student might make.
Some of these errors are a stretch. One of the golden rules for writing a good diagnostics question is you want each choice of the wrong answers to capture one and only one misconception so you can be confident in your diagnosis of where the student has gone wrong.
So, can an AI chatbot write a good multiple-choice diagnostic question?
Yes… but they struggled more than they did with last week’s task.
At first glance, that might be a surprise. After all, creating a diagnostic question is intrinsically related to predicting misconceptions, and the chatbtos are pretty good at the latter. But, creating a good diagnostic question is not just about anticipating student misconceptions; it is also about creating plausible distractors that will draw out these misconceptions and doing so for the same single starting point. It turns out that this is quite a cognitive leap.
On a technical level, these AI chatbots are trained on large data sets comprised mainly of correct responses. Hence, the notion of thinking where students may go wrong and responding with an appropriate answer choice lies somewhat outside of their wheelhouse. A parallel can be drawn here with the novice teacher whose only experience of maths is in top sets surrounded by lots of correct answers.
Nevertheless, I was impressed with ChatGTP and Claude's output. ChatGTP's nailing of the maths notation puts it—as it was last week—in the lead. And, of course, both chatbots wrote their questions in a fraction of the time it takes me - and I am pretty quick.
But we must be cautious. Writing misconceptions about adding fractions is relatively straightforward for an experienced teacher. How would the chatbots cope with writing questions about plotting straight-line graphs, interpreting bar models, or carrying out loci and constructions? Well, we do not know because none of the chatbots currently can produce images. Hence, they cannot provide good diagnostic questions on most geometry topics, graphs, or statistical diagrams.
Most importantly, as we also saw last week, chatbots make mistakes, no matter how sure of themselves they initially sound. Unless you spot these mistakes and inform the chatbots, they will remain blissfully unaware. Just as you (hopefully!) wouldn’t download a PowerPoint from the internet and use it straight away in class without looking at it first, any output from chatbots needs to be carefully checked to avoid those hallucinations that are so confidently spewed out.
But when I write my next diagnostic question, I will first try ChatGTP and Claude. I suspect they will consistently give me a good starting point, and I look forward to their performance improving in the near future. But I will postpone my question-writing retirement and subsequent beach holiday for now.
Want to know more?
Next week, we will look at something even more complex than creating a diagnostic question - and the results are surprising - so stay tuned for that. In addition, I heartily recommend signing up for Neil Almond’s free teacher-focussed AI newsletter. Each week, he compiles the latest AI developments and also shares a prompt you can use right away that might save you time, help you do your job better, or maybe both!
Have you used a Chatbot to aid your teaching?
What worked, and what didn’t?
Let me know in the comments below!
🏃🏻♂️ Before you go, have you…🏃🏻♂️
… checked out our incredible, brand-new, free resources from Eedi?
… read my latest Tips for Teachers newsletter about reducing the content demands of a new routine?
… listened to my most recent podcast with Ollie Lovell about a recent lesson he taught?
… considered booking some CPD, coaching, or maths departmental support?
… read my Tips for Teachers book?
Thanks so much for reading and have a great week!
Craig